The delta-function Potential Lattice

I was messing around with some simple problems, and found this simple but illustrative problem. It starts you off in basic quantum mechanics and introduces concepts in a very straightforward way to both get to a more condensed matter perspective while even showing some interesting effects that have experimental consequences (energy bands and band gaps opening).

We look at the relatively simple problem¹ of finding the energy spectrum for a particle in the lattice potential

\begin{equation} U(x) = \alpha\sum_{n=-\infty}^\infty \delta(x - n a)\end{equation}.

The time-independent Schrödinger equation takes the form

\begin{equation} \left[ - \frac{\partial_x^2}{ 2 m} + U(x) \right] \psi(x) = E \psi(x),\end{equation}

where \(E\) is the energy.

Since we can solve the problem between the delta-functions quite simply (\(U(x) =0\) there), let us restrict our focus to \(na \lt x \lt (n+1)a\). Here, the wave function takes on the form

\begin{equation} \psi(x) = A_n e^{ik(x-na)} + B_n e^{-ik(x-na)},\end{equation}

where we have \(k = \sqrt{2m E}\). Now, we can find an operator that commutes with the Hamiltonian so that we can diagonlize it to help solve the problem — this will be the operator that translates us by \(a\).

To make this clear, let us abstract things to operators so that we have a momentum operator \(p\) and a position operator \(x\), then we have the commutator \([ x, p] = i\). The operator \(p\) commutes with functions of \(x\) as though it were a derivative \([ p, f( x)] = -i f'( x)\), so considering the translation operator \(e^{i a p }\), we can write

\begin{equation} e^{i a p} U( x) e^{ - i a p} = \sum_{n=0}^\infty \frac1{n!} U^{(n)}( x) a^n = U( x + a),\end{equation}

and since \(U(x)\) is periodic in \(a\), we have that \(e^{i a p} U( x) e^{ - i a p} = U( x)\). Thus, the operator \(T_a = e^{i a p}\) commutes with the Hamiltonian and we can simulataneously diagonalize both it and the Hamiltonian. We say \(T_a \lvert \psi\rangle = e^{i a q} \lvert \psi \rangle\) has quasi-momentum \(q\). It is important to note that this not the same as real momentum which is not a well-defined quantum number in this problem (that needs translation symmetry).

In other words, we can write our eigenfunctions such that \(\psi(x+a) = e^{i q a} \psi(x)\), and this naturally leads us to relate the coefficients for our eigenfunctions above as

\begin{equation} A_{n-1} = e^{-i q a} A_n, \quad B_{n-1} = e^{-i q a} B_n.\end{equation}

Now, we can apply matching conditions at \(x = na\) remembering that our wavefunction should be continuous, but that the delta-function will cause the first derivatives to be discontinuous. The equations for the coefficients are

\begin{align} A_n + B_n & = e^{i k a} A_{n-1} + e^{-i k a} B_{n-1}, \\
\left( 1 + \frac{2 i m \alpha}{k} \right) A_n - \left( 1 - \frac{2 i m \alpha}k \right) B_n & = e^{i k a} A_{n-1} - e^{-ik a} B_{n-1}, \end{align}

and if we insert the relation between the coefficients at \(n-1\) and \(n\), we get a matrix equation

\begin{align} \begin{pmatrix} e^{i q a} - e^{i k a} & e^{i q a} - e^{- i k a} \\
e^{i q a} \left(1 + \tfrac{2 i m \alpha}k \right) - e^{i k a} & - e^{i q a } \left( 1 - \tfrac{2 i m \alpha}k \right) + e^{-ik a} \end{pmatrix} \begin{pmatrix} A_n \ B_n \end{pmatrix} = 0. \end{align}

This equation has a non-zero solution only if the determinant of the matrix is zero which can be written as

\begin{equation} \cos q a - f(E) = 0 , \quad f(E) = \cos ka + \frac{m \alpha}{k} \sin ka. \end{equation}

This is an equation which relates the energy to the quasi-momentum. Since \(\cos q a\) can only be between -1 and 1, this equation only has a solution when \(f(E)\) is between -1 and 1. The oscillatory nature of \(f(E)\) means that it should pass in this range multiple (in fact, a countable infinite) number of times.

Armed with this equation, we can use \(q\) and an integer to label our energies and we obtain the following energy bands by just solving for \(E\) (setting \(m = 10\), \(a = 1\), and \(\alpha = 0.3\))

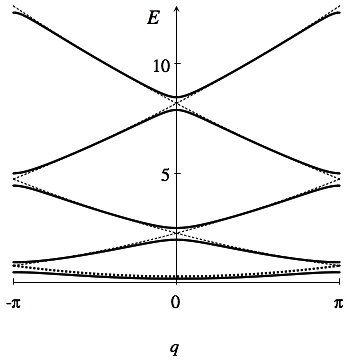
The dotted lines in this plot represent the spectrum if there were no delta-function potentials (displaced in energy by \(\alpha / a\) for clarity). Notice how the introduction of the delta-functions opens up gaps in this energy spectrum, so that there are some energies that are inaccessible. The gaps actually open up when \(\lvert f(E)\rvert \geq 1\) since there is no solution to our equation there. This energy gap for small \(\alpha\) just goes like \(\alpha/a\), vanishing as we’d expect when \(\alpha = 0\).

Notice that in this energy spectrum, we see that if \(q \rightarrow -q\) we get the same energy.

Additionally, if the energy ever goes negative the solutions turn from plane waves \(e^{\pm i k (x-na)}\) into functions localized around the delta functions \(e^{\pm\kappa(x-na)}\). In fact, the wave functions look like this for a \(q=0\) state:

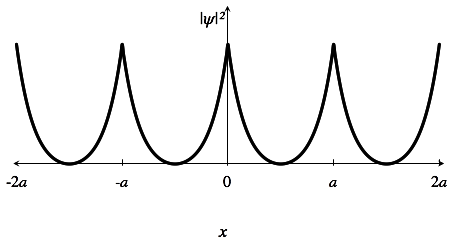
These only appear when \(\alpha \lt 0\), and are related to the fact that the delta-function potential has a bound state. Additionally, only one band can ever have this state. This is due to the fact that the oscillatory sine and cosine change to their non-oscillatory hyperbolic counterparts. However, these states in the delta-function lattice are spread out throughout the crystal, and can not be said to be “localized” to a specific site — they still all have a definite quasi-momentum.

As with other single particle problems, upon considering the many particle picture, these energy bands get filled up to a set energy level (if we are considering fermions).