For applications in many parts of condensed matter physics and cold atoms physics, we use what is known as the Rashba spin-orbit coupled Hamiltonian. This Hamiltoninan is so-named because it couples momentum \(\mathbf{p}\) to the spin \(\mathbf{S}=\frac12\sigma\) where \(\sigma = (\sigma_x,\sigma_y,\sigma_z)\) are the Pauli matrices and \(\mathbf{p}=(p_x,p_y,p_z)\) is a vector of momentum operators:

\begin{equation} H = \frac{p^2}{2m} + \alpha (\boldsymbol{\sigma} \times \mathbf{p})\cdot \hat{\mathbf{z}} + \Delta \sigma_z. \end{equation}

\(m\) is the mass, \(\alpha\) is the spin-orbit coupling strength, and \(\Delta\) is some Zeeman field (it acts as magnetic field on the spin).

In this post, we go through the calculation of the energy spectrum and eigenvectors – a straight forward exercise in undergraduate linear algebra.

First of all, instead of the normal method of finding eigenvectors, we note that we can rewrite this Hamiltonian in the form

\begin{equation} H = \frac{p^2}{2m} + \mathbf{b}(p) \cdot \boldsymbol{\sigma} \end{equation}

where \(\mathbf{b}(p) = (\alpha p_y, -\alpha p_x, \Delta)\). Now, \(\mathbf{b}(p)\) represents a point on the Bloch sphere, and so we expect the eigenvectors to be parallel and anti-parallel to this vector. The energies in this case are very straight forward and amount to the positive and negative of \(\lvert\mathbf{b}(p)\rvert\):

\begin{equation} \epsilon_\pm(p) = \frac{p^2}{2m} \pm \sqrt{ \alpha^2 p^2 + \Delta^2}. \end{equation}

With these eigenvalues, it is a straight forward exercise in linear algebra to find the eigenvectors. After a bit of algebra, the eigenvectors of \(H\) in terms of the eigenvectors of \(\sigma_z\) ( \(\sigma_z\left\lvert\uparrow\right\rangle = \left\lvert\uparrow\right\rangle\) and \(\sigma_z\left\lvert\uparrow\right\rangle = -\left\lvert\uparrow\right\rangle\) ) are

\begin{equation}\left\lvert\pm\right\rangle = \frac1{\sqrt2}\left[\sqrt{1 \pm \frac{\Delta}{\sqrt{\Delta^2+\alpha^2 p^2}}}\left\lvert\uparrow\right\rangle + e^{-i\phi} \sqrt{1 \mp \frac{\Delta}{\sqrt{\Delta^2+\alpha^2 p^2}}}\left\lvert\downarrow\right\rangle \right]\end{equation}

where we have defined \(\phi\) by \(p_y+ip_x = p e^{i\phi}\). Note that when \(p_{x,y} \rightarrow -p_{x,y}\), the occupations stay the same. However, if we just look at one energy, \(\epsilon_-(p)\) the ground state energy, we see that the state we get when \(p_{x,y} \rightarrow -p_{x,y}\) is almost orthogonal to the original state.

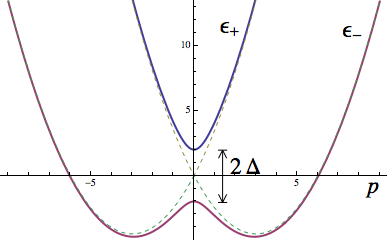
The energy bands themselves look like the figure on the right where the vertical axis is energy (and for this particular example, \(m=1\), \(\alpha = 3\), and \(\Delta=2\)). Interestingly, the introduction of \(\Delta\) actually causes the gap to open up – the dotted lines are for when \(\Delta=0\).

Now, if we have a bunch of fermions filling up these energies, if we set the chemical potential to be in the gap, we would find that the only excitations would states that are spin-locked to the momentum.

Many things can be done with this Hamiltonian to interesting effect. It finds its way into cold atom physics as well as condensed matter.