In models that naturally have a continuum, it is sometimes possible to find bound states with the application of a potential well. These states don’t come out of nowhere though and since they are combinations of continuum states, the continuum itself is altered. To begin to understand how the continuum is altered, we look at the simplest example here: A \(\delta\)-function potential in one-dimension and with quadratic dispersion.

\[\begin{equation} -\frac1{2m} \psi''(x) - \lambda \delta(x) \psi(x) = E \psi(x). \label{eq:schro} \end{equation}\]

The general strategy here is to convert this potential into a matching condition between left and right parts of space. In particular, if we integrate \(x\) from \(0^-\) to \(0^+\), we get

\[\begin{equation} -\frac1{2m}[\psi'(0^+) - \psi'(0^-)] = \lambda \psi(0). \label{eq:matching} \end{equation}\]

The bound state solution to this problem is a simple exponential

\[\begin{equation} \psi_0(x) = \sqrt{m\lambda}\, e^{- m\lambda |x|}, \quad E= -\tfrac12 m\lambda^2 \end{equation}\]
Expand for derivation

We require the bound state to be square integrable, so \(\psi_0(x) = \mathcal N e^{-\kappa x}\) for \(x>0\) and \(\psi_0(x) = \mathcal N e^{\kappa x}\) for \(x<0\). In both cases, we can evaluate \eqref{eq:schro}

\[\begin{equation} -\frac{\kappa^2}{2m} \psi_0(x) = E\psi_0(x), \quad \implies \kappa = \sqrt{-2mE}. \label{eq:bs_energy} \end{equation}\]

Using our forms of \(\psi_0(x)\) on either side of zero, we have \(\psi_0'(0^+) = - \kappa \psi_0(0)\) and \(\psi_0(0^-) = +\kappa \psi_0(0)\). Putting these into \eqref{eq:matching}, we have

\[\begin{equation} \frac{\kappa}{m} \psi_0(0) = \lambda \psi_0(0). \end{equation}\]

This means that \(\kappa = \lambda m\), and matching this to \eqref{eq:bs_energy} we find \(E = -\frac12 m \lambda^2\). All that is left is normalization and simply

\[\begin{equation} \begin{aligned} 1 & = \int dx |\psi_0(x)|^2 \\ & = 2 \int_0^\infty dx \mathcal N^2 e^{-2\kappa x} \\ & = \frac{\mathcal N^2}{\kappa}. \end{aligned} \end{equation}\]

This gives us \(\mathcal N = \sqrt{\kappa} = \sqrt{\lambda m}\), completing our derivation.

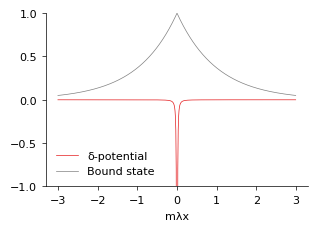
The delta function potential (red) along with the resulting bound state (gray).

But what about the continuum? First, sine waves automatically satisfy \eqref{eq:schro}, and we have

\[\begin{equation} \psi^s_k(x) = \sin(k x), \quad E = \frac{k^2}{2m}. \end{equation}\]

It is worth noting that these wave functions are normalized such that

\[\begin{equation} \int dx\; \psi^s_k(x)\psi^s_{k'}(x) = \pi \delta(k - k') \end{equation}\]

The continuum states that are modified are the cosine waves

\[\begin{equation} \psi_k^c(x) = \frac{1}{\sqrt{1+\lambda^2m^2/k^2}} \left[\cos(k x) - \frac{\lambda m}{k} \sin | kx|\right], \quad E = \frac{k^2}{2m}. \end{equation}\]

This is again chosen such that \(\int dx \; \psi_k^c(x) \psi_{k'}^c(x) = \pi \delta(k - k')\).

Expand for derivation

First, \(\psi_k^s(x) = \sin(k x)\) is a complete basis for antisymmetric wavefunctions, and therefore, we know that \(\psi_k^c(-x) = \psi_k^c(x)\) in order to maintain orthogonality with \(\psi_k^s(x)\). This implies that if for \(x>0\) we have \(\psi_k^c(x) = A \cos(kx) + B \sin(kx)\), then for \(x<0\), \(\psi_k^c(x) = A \cos(kx) - B \sin(kx)\) justifying our functional form.

We have already guaranteed continuity across \(x=0\), so now we just need to satisfy the matching conditions \eqref{eq:matching} for which we have \({\psi_k^{c}}'(0^+) = B k\) and \({\psi_k^{c}}'(0^-) = -B k\) and therefore by \eqref{eq:matching}

\[\begin{equation} - \frac{B k}m = A \lambda \quad \implies \quad B = -\frac{\lambda m}{k} A \end{equation}\]

All that is left is normalization (fixing \(A\)). For this, we introduce a regulator \(e^{-\delta \lvert x \rvert}\) and take it to be small

\[\begin{equation} \begin{aligned} \int dx \, \psi_k^c(x) \psi_{p}^c(x) e^{-\delta |x|} & = 2 A^2 \int_0^\infty dx \, \left(\cos k x - \frac{\lambda m}{k} \sin kx \right)\left(\cos p x - \frac{\lambda m}{p} \sin px \right)e^{-\delta x} \\ & = 2A^2 \frac{\delta (k^2 + p^2 + \delta^2 - 2\delta \lambda^2 m^2 + 2 \lambda^4 m^4)}{(k^2 - p^2)^2 + 2 (k^2 + p^2)\delta^2 + \delta^4} \end{aligned} \end{equation}\]

If \(k \neq p\), then this expression goes to zero as \(\delta \rightarrow 0\), and it appears to diverge with \(1/\delta\) if \(k = p\), a hallmark of a Dirac delta function. In fact, making sure this integrates to \(\pi\) when we integrate with respect to \(k\) or \(p\) gives us exactly

\[\begin{equation} \int_0^\infty dp \, 2A^2 \frac{\delta (k^2 + p^2 + \delta^2 - 2\delta \lambda^2 m^2 + 2 \lambda^4 m^4)}{(k^2 - p^2)^2 + 2 (k^2 + p^2)\delta^2 + \delta^4} = A^2 \pi \frac{(\lambda^2 m^2 + k^2 - \lambda m \delta + \delta^2)}{k^2 + \delta^2} \end{equation}\]

As \(\delta \rightarrow 0\) then, we obtain

\[\begin{equation} A = \frac1{\sqrt{1 + \lambda^2 m^2/k^2}}, \end{equation}\]

completing this derivation.

Taken together, we can now define the (local) density of states for the continuum

\[\begin{equation} \rho(E; x) = \int_0^\infty \frac{dk}{\pi} (|\psi_k^c(x)|^2 + |\psi_k^s(x)|^2) \delta(E - k^2/(2m)) \end{equation}\]

To address this, we want to find the difference from the continuum which we call

\[\begin{equation} \rho_0(E;x) = \int_0^\infty\frac{dk}{\pi} (\cos^2(kx) + \sin^2(kx)) \delta(E - k^2/(2m)) \end{equation}\]

Subtracting these

\[\begin{equation} \Delta \rho(E; x) = \rho(E;x) - \rho_0(E; x), \end{equation}\]

With a bit of work, we can find

\[\begin{equation} \Delta \rho(\tfrac{k^2}{2m}; x) = - \frac{m}{k\pi} \frac{(m \lambda )^2 \cos (2kx) + m \lambda k \sin|2kx|}{(m \lambda)^2 + k^2}. \end{equation}\]

We can finally, integrate this over all energies

\[\begin{equation} \int_0^\infty dE \; \Delta \rho(E; x) = - m\lambda e^{-2 m\lambda |x|} = - |\psi_0(x)|^2. \end{equation}\]

As you might suspect: the continuum is depleted in the exact way to compensate the bound state. This is known as the Friedel sum rule. But which continuum states are playing the largest roles? For this, we can take

\[\Delta \rho(E) \equiv \lim_{\delta\rightarrow0^+}\int dx \, \Delta \rho(E,x) e^{-\delta |x|},\]

from which we find

\[\begin{equation} \Delta \rho(E)dE = \left[-\frac12\delta(k - 0^+) - \frac{1}{\pi} \frac{m\lambda }{(m\lambda)^2 + k^2} \right] dk, \quad E = \frac{k^2}{2m} \end{equation}\]

We can tell from this that half of the weight comes from the \(k=0\) (constant) mode. The rest of the weight comes from higher \(k\)’s distributed like a Lorentzian. If we include the ground state as a positive \(\delta\)-function, we get:

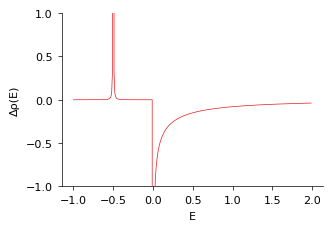
The change in density of states for with delta functions artificially broadened to make them visible. This function integrates to zero: the Friedel sum rule in action.

This is a simple example of how charge can be pulled from the continuum to make a bound state: leaving a depletion of density in the continuum.